Fitness landscape
| Part of a series on |
| Evolutionary biology |
|---|
 |
In evolutionary biology, fitness landscapes or adaptive landscapes (types of evolutionary landscapes) are used to visualize the relationship between genotypes and reproductive success. It is assumed that every genotype has a well-defined replication rate (often referred to as fitness). This fitness is the "height" of the landscape. Genotypes which are similar are said to be "close" to each other, while those that are very different are "far" from each other. The set of all possible genotypes, their degree of similarity, and their related fitness values is then called a fitness landscape. The idea of a fitness landscape is a metaphor to help explain flawed forms in evolution by natural selection, including exploits and glitches in animals like their reactions to supernormal stimuli.
The idea of studying evolution by visualizing the distribution of fitness values as a kind of landscape was first introduced by Sewall Wright in 1932.[1]
In evolutionary optimization problems, fitness landscapes are evaluations of a fitness function for all candidate solutions (see below).
In biology[edit]
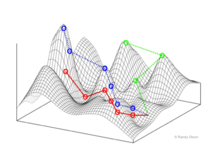
In all fitness landscapes, height represents and is a visual metaphor for fitness. There are three distinct ways of characterizing the other dimensions, though in each case distance represents and is a metaphor for degree of dissimilarity.[2]
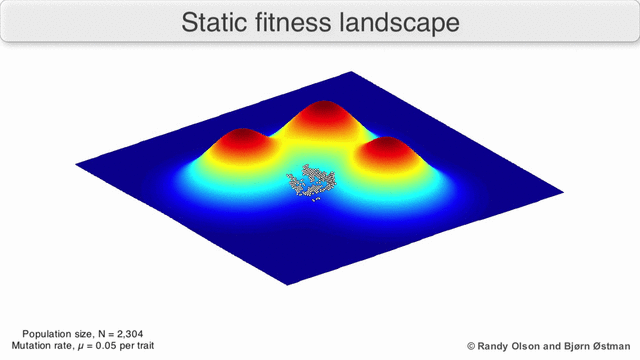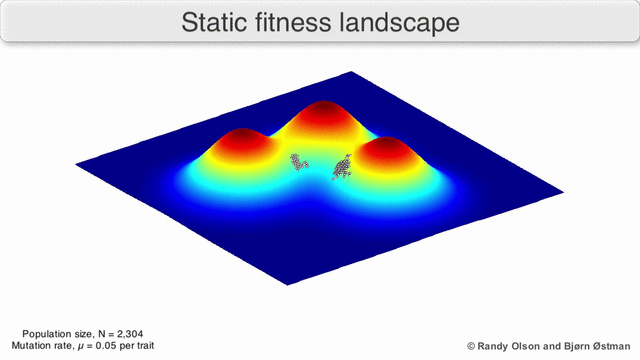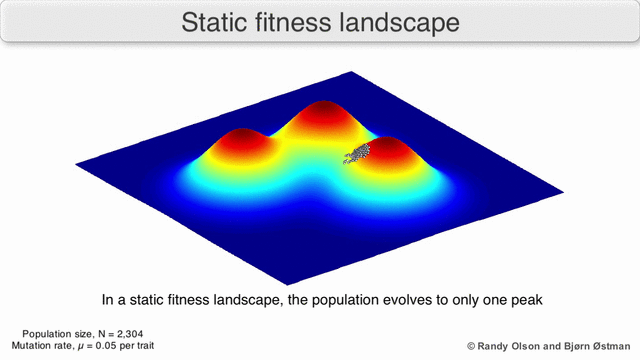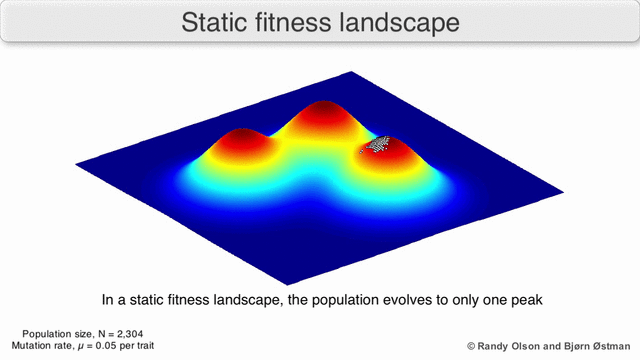
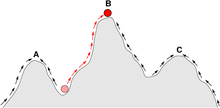
Fitness landscapes are often conceived of as ranges of mountains. There exist local peaks (points from which all paths are downhill, i.e. to lower fitness) and valleys (regions from which many paths lead uphill). A fitness landscape with many local peaks surrounded by deep valleys is called rugged. If all genotypes have the same replication rate, on the other hand, a fitness landscape is said to be flat. An evolving population typically climbs uphill in the fitness landscape, by a series of small genetic changes, until – in the infinite time limit – a local optimum is reached.
Note that a local optimum cannot always be found even in evolutionary time: if the local optimum can be found in a reasonable amount of time then the fitness landscape is called "easy" and if the time required is exponential then the fitness landscape is called "hard".[3] Hard landscapes are characterized by the maze-like property by which an allele that was once beneficial becomes deleterious, forcing evolution to backtrack. However, the presence of the maze-like property in biophysically inspired fitness landscapes may not be sufficient to generate a hard landscape.[4]
Genotype to fitness landscapes[edit]
Wright visualized a genotype space as a hypercube.[1] No continuous genotype "dimension" is defined. Instead, a network of genotypes are connected via mutational paths.
Stuart Kauffman's NK model falls into this category of fitness landscape. Newer network analysis techniques such as selection-weighted attraction graphing (SWAG) also use a dimensionless genotype space.[5]
Allele frequency to fitness landscapes[edit]
Wright's mathematical work described fitness as a function of allele frequencies.[2] Here, each dimension describes an allele frequency at a different gene, and goes between 0 and 1.
Phenotype to fitness landscapes[edit]
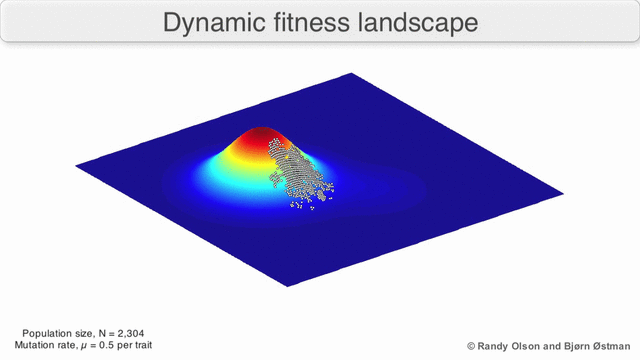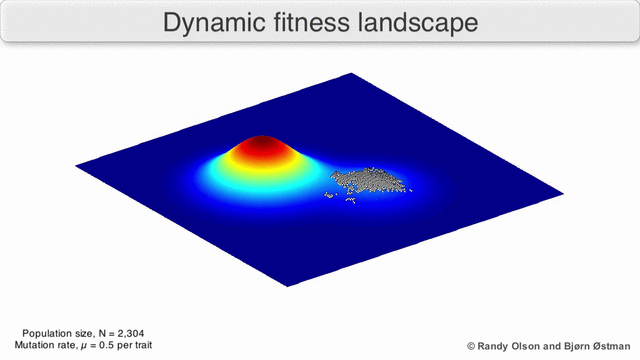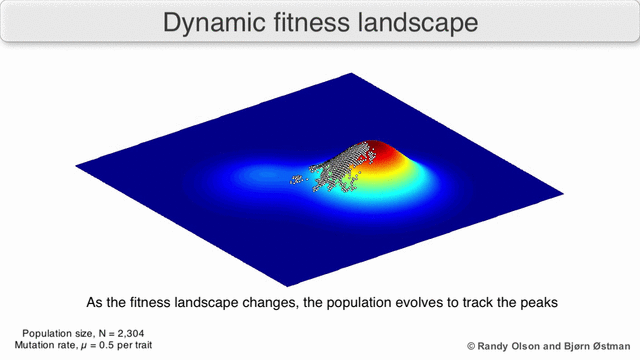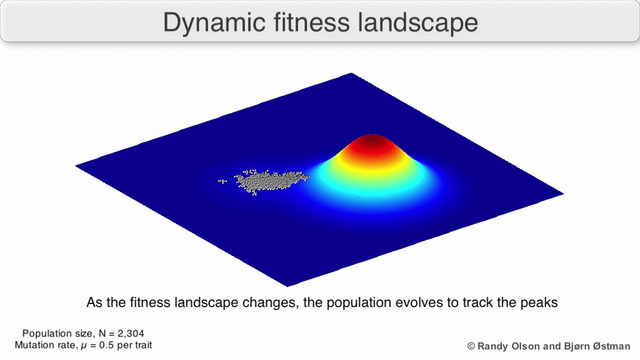
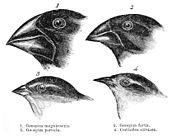
In the third kind of fitness landscape, each dimension represents a different phenotypic trait.[2] Under the assumptions of quantitative genetics, these phenotypic dimensions can be mapped onto genotypes. See the visualizations below for examples of phenotype to fitness landscapes.
In evolutionary optimization[edit]
Apart from the field of evolutionary biology, the concept of a fitness landscape has also gained importance in evolutionary optimization methods such as genetic algorithms or evolution strategies. In evolutionary optimization, one tries to solve real-world problems (e.g., engineering or logistics problems) by imitating the dynamics of biological evolution. For example, a delivery truck with a number of destination addresses can take a large variety of different routes, but only very few will result in a short driving time.
In order to use many common forms of evolutionary optimization, one has to define for every possible solution s to the problem of interest (i.e., every possible route in the case of the delivery truck) how 'good' it is. This is done by introducing a scalar-valued function f(s) (scalar valued means that f(s) is a simple number, such as 0.3, while s can be a more complicated object, for example a list of destination addresses in the case of the delivery truck), which is called the fitness function.
A high f(s) implies that s is a good solution. In the case of the delivery truck, f(s) could be the number of deliveries per hour on route s. The best, or at least a very good, solution is then found in the following way: initially, a population of random solutions is created. Then, the solutions are mutated and selected for those with higher fitness, until a satisfying solution has been found.
Evolutionary optimization techniques are particularly useful in situations in which it is easy to determine the quality of a single solution, but hard to go through all possible solutions one by one (it is easy to determine the driving time for a particular route of the delivery truck, but it is almost impossible to check all possible routes once the number of destinations grows to more than a handful).
Even in cases where a fitness function is hard to define, the concept of a fitness landscape can be useful. For example, if fitness evaluation is by stochastic sampling, then sampling is from a (usually unknown) distribution at each point; nevertheless is can be useful to reason about the landscape formed by the expected fitness at each point. If fitness changes with time (dynamic optimisation) or with other species in the environment (co-evolution), it can still be useful to reason about the trajectories of the instantaneous fitness landscape. However, in some cases (for example, preference-based interactive evolutionary computation) the relevance is more limited, because there is no guarantee that human preferences are consistent with a single fitness assignment.
The concept of a scalar valued fitness function f(s) also corresponds to the concept of a potential or energy function in physics. The two concepts only differ in that physicists traditionally think in terms of minimizing the potential function, while biologists prefer the notion that fitness is being maximized. Therefore, taking the inverse of a potential function turns it into a fitness function, and vice versa.[6]
Caveats and limitations[edit]
Several important caveats exist. Since the human mind struggles to think in greater than three dimensions, 3D topologies can mislead when discussing highly multi-dimensional fitness landscapes.[7][8] In particular it is not clear whether peaks in natural biological fitness landscapes are ever truly separated by fitness valleys in such multidimensional landscapes, or whether they are connected by vastly long neutral ridges.[9][10] Additionally, the fitness landscape is not static in time but dependent on the changing environment and evolution of other genes.[5] It is hence more of a seascape,[11] further affecting how separated adaptive peaks can actually be. Additionally, it is relevant to take into account that a landscape is in general not an absolute but a relative function.[12] Finally, since it is common to use function as a proxy for fitness when discussing enzymes, any promiscuous activities exist as overlapping landscapes that together will determine the ultimate fitness of the organism, implying a gap between different coexisting relative landscapes.[13]
With these limitations in mind, fitness landscapes can still be an instructive way of thinking about evolution. It is fundamentally possible to measure (even if not to visualise) some of the parameters of landscape ruggedness and of peak number, height, separation, and clustering. Simplified 3D landscapes can then be used relative to each other to visually represent the relevant features. Additionally, fitness landscapes of small subsets of evolutionary pathways may be experimentally constructed and visualized, potentially revealing features such as fitness peaks and valleys.[5] Fitness landscapes of evolutionary pathways indicate the probable evolutionary steps and endpoints among sets of individual mutations.
See also[edit]
References[edit]
- ^ a b Wright, Sewall (1932). "The roles of mutation, inbreeding, crossbreeding, and selection in evolution" (PDF). Proceedings of the Sixth International Congress on Genetics. 1 (8): 355–66.
- ^ a b c Provine, William B. (1986). Sewall Wright and Evolutionary Biology. University of Chicago Press.[page needed]
- ^ Kaznatcheev, Artem (2019). "Computational Complexity as an Ultimate Constraint on Evolution". Genetics. 212 (1): 245–265. doi:10.1534/genetics.119.302000. PMC 6499524. PMID 30833289.
- ^ Bertram, Jason; Masel, Joanna (April 2020). "Evolution Rapidly Optimizes Stability and Aggregation in Lattice Proteins Despite Pervasive Landscape Valleys and Mazes". Genetics. 214 (4): 1047–1057. doi:10.1534/genetics.120.302815. PMC 7153934. PMID 32107278.
- ^ a b c Steinberg, B; Ostermeier, M (2016). "Environmental changes bridge evolutionary valleys". Science Advances. 2 (1): e1500921. Bibcode:2016SciA....2E0921S. doi:10.1126/sciadv.1500921. PMC 4737206. PMID 26844293.
- ^ Kauffman, Stuart A. (1993). The origins of order, self-organization and selection in evolution (1st ed.). New york - Oxford: Oxford University Press. p. 43. ISBN 0-19-505811-9.
- ^ McCandlish, David M (2011). "Visualizing Fitness Landscapes". Evolution. 65 (6): 1544–58. doi:10.1111/j.1558-5646.2011.01236.x. PMC 3668694. PMID 21644947.
- ^ McGhee, George R. (2006). The Geometry of Evolution: Adaptive Landscapes and Theoretical Morphospaces. Cambridge University Press. ISBN 978-1-139-45995-2.[page needed]
- ^ Gavrilets, S. (2004). Fitness Landscapes and the Origin of Species. Princeton University Press. ISBN 978-0-691-11983-0.[page needed]
- ^ Kaplan, Jonathan (2008). "The end of the adaptive landscape metaphor?". Biology & Philosophy. 23 (5): 625–38. doi:10.1007/s10539-008-9116-z. S2CID 170649453.
- ^ Mustonen, Ville; Lässig, Michael (2009). "From fitness landscapes to seascapes: Non-equilibrium dynamics of selection and adaptation". Trends in Genetics. 25 (3): 111–9. doi:10.1016/j.tig.2009.01.002. PMID 19232770.
- ^ Woodcock, Glenn; Higgs, Paul G (1996). "Population Evolution on a Multiplicative Single-Peak Fitness Landscape". Journal of Theoretical Biology. 179 (1): 61–73. doi:10.1006/jtbi.1996.0049. PMID 8733432.
- ^ Diaz Ochoa, Juan G (2017). "Elastic Multi-scale Mechanisms: Computation and Biological Evolution". Journal of Molecular Evolution. 86 (1): 47–57. Bibcode:2018JMolE..86...47D. doi:10.1007/s00239-017-9823-7. PMID 29248946. S2CID 22624633.
External links[edit]
- Examples of visualized fitness landscapes
- Video: Using fitness landscapes to visualize evolution in action
- BEACON Blog—Evolution 101: Fitness Landscapes
- Pleiotropy Blog—an interesting discussion of Sergey Gavrilets's contributions
- Pup Fish Evolution—UC Davis
- Evolution 101—Shifting Balance Theory (Figure at bottom of page)
- Superimposing evolutionary trajectories onto fitness landscapes in virtual reality
- Further reading
- Counterbalance: Evolution as movement through a fitness landscape—an interesting (if flawed) discussion of evolution and fitness landscapes
- Example of the use of Evolutionary Landscapes in thinking & speaking about evolution
- Hendrik Richter; Andries P. Engelbrecht (2014). Recent Advances in the Theory and Application of Fitness Landscapes. Springer. ISBN 978-3-642-41888-4.
- Beerenwinkel, Niko; Pachter, Lior; Sturmfels, Bernd (2007). "Epistasis and Shapes of Fitness Landscapes". Statistica Sinica. 17 (4): 1317–42. arXiv:q-bio.PE/0603034. Bibcode:2006q.bio.....3034B. MR 2398598.
- Richard Dawkins (1996). Climbing Mount Improbable. Norton. ISBN 0-393-03930-7.
- Sergey Gavrilets (2004). Fitness landscapes and the origin of species. Princeton University Press. ISBN 978-0-691-11983-0.
- Stuart Kauffman (1995). At Home in the Universe: The Search for Laws of Self-Organization and Complexity. Oxford University Press, USA. ISBN 978-0-19-511130-9.
- Melanie Mitchell (1996). An Introduction to Genetic Algorithms (PDF). MIT Press. ISBN 978-0-262-63185-3.
- Langdon, W. B.; Poli, R. (2002). "Chapter 2 Fitness Landscapes". Foundations of Genetic Programming. Springer. ISBN 3-540-42451-2.
- Stuart Kauffman (1993). The Origins of Order. Oxford University Press. ISBN 978-0-19-507951-7.
- Poelwijk, Frank J; Kiviet, Daniel J; Weinreich, Daniel M; Tans, Sander J (2007). "Empirical fitness landscapes reveal accessible evolutionary paths". Nature. 445 (7126): 383–6. Bibcode:2007Natur.445..383P. doi:10.1038/nature05451. PMID 17251971. S2CID 4415468.
- Bukkuri A, Pienta KJ, Hockett I, Austin RH, Hammarlund EU, Amend SR, Brown JS. Modeling cancer's ecological and evolutionary dynamics. Med Oncol. 2023 Feb 28;40(4):109. doi: 10.1007/s12032-023-01968-0. PMID: 36853375; PMCID: PMC9974726.