Topologist's sine curve
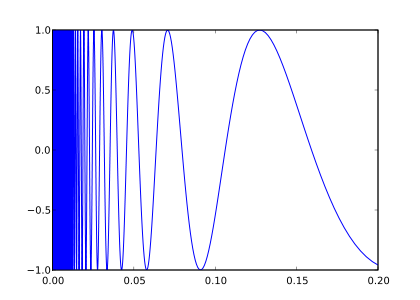
In the branch of mathematics known as topology, the topologist's sine curve or Warsaw sine curve is a topological space with several interesting properties that make it an important textbook example.
It can be defined as the graph of the function sin(1/x) on the half-open interval (0, 1], together with the origin, under the topology induced from the Euclidean plane:
![{\displaystyle T=\left\{\left(x,\sin {\tfrac {1}{x}}\right):x\in (0,1]\right\}\cup \{(0,0)\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d4221bd712b70257f7e0f8d9b1ca74eaff5661c)
Properties[edit]
The topologist's sine curve T is connected but neither locally connected nor path connected. This is because it includes the point (0,0) but there is no way to link the function to the origin so as to make a path.
The space T is the continuous image of a locally compact space (namely, let V be the space {−1} ∪ (0, 1], and use the map f from V to T defined by f(−1) = (0,0) and f(x) = (x, sin(1/x)) for x > 0), but T is not locally compact itself.
The topological dimension of T is 1.
Variants[edit]
Two variants of the topologist's sine curve have other interesting properties.
The closed topologist's sine curve can be defined by taking the topologist's sine curve and adding its set of limit points, ; some texts define the topologist's sine curve itself as this closed version, as they prefer to use the term 'closed topologist's sine curve' to refer to another curve.[1] This space is closed and bounded and so compact by the Heine–Borel theorem, but has similar properties to the topologist's sine curve—it too is connected but neither locally connected nor path-connected.
![{\displaystyle \{(0,y)\mid y\in [-1,1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3dff9ac5c2a53868d76f8bf3f7a7a841876b3ca0)
The extended topologist's sine curve can be defined by taking the closed topologist's sine curve and adding to it the set . It is arc connected but not locally connected.
![{\displaystyle \{(x,1)\mid x\in [0,1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5327e8b84efd6909fc334b522974b34963cd7e8f)
See also[edit]
References[edit]
- ^ Munkres, James R (1979). Topology; a First Course. Englewood Cliffs. p. 158. ISBN 9780139254956.
- Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978], Counterexamples in Topology (Dover reprint of 1978 ed.), Mineola, NY: Dover Publications, Inc., pp. 137–138, ISBN 978-0-486-68735-3, MR 1382863
- Weisstein, Eric W. "Topologist's Sine Curve". MathWorld.